网络残缺度：共同好友间可否两步到达？

网络是由节点和关系构成的，而对于关系的描述是社会网络的关键。我们已经知道对于节点的网络特性可以从中心度、近度、介度、特征度（eigenvalue centrality）等方式描述。那么对于关系呢？最简单的就是直接关系的强度了。

关系强度（tie strength)

通常对于关系强度的测量是基于两个节点之间链接的权重来衡量的。并不是说关系的强度越高越好，也不是说越多的强关系就越好。例如，格兰诺维特的论文The strength of weak ties强调了弱关系的重要性。

共同好友（common friends）

但是以直接的链接强度度量一对关系的强度显然过于简单。它忽略的网络中的三角形（triads）：网络的局部传递性(transtivity)。关系的传递性是社会网络分析的一种重要观点。比如，朋友的朋友成为自己的朋友的可能性很高。这种关系的强度不只限于一模网络中。在传播学中有ABX模型，A和B是两个人，X是一种对象（信息、意见、创新等）。A和B是好朋友，A喜欢X，那么B喜欢X的可能性就提高。也就是爱朋友及朋友喜欢的东西，有点像爱屋及乌。

怎么抓住网络的传递性？找两个节点(一对关系)的共同好友！找到共同好友就抓住了网络中的三角形。存在的三角形数量就表明了传递性的程度。这种思路其实对于做共引（co-citation)分析的学者来说并不陌生。如果一篇论文同时引用了两篇论文，那么这两篇论文就存在一定的相似性。因此，找共同好友类似于找共引关系。

嵌入度（embededness）

共同好友数量是判断两个人亲密程度的一个重要变量。如果共同好友的数量足够多，表明这两个人彼此深度的融入了对方的社会关系当中。基于这种思路，我们可以计算嵌入型。对于i和j两个人, $k_{i}$、$k_{j}$分别表示i和j的好友数量。$n_{ij}$表示其共同好友数量。那么，我们可以如下计算嵌入度：

\[Embededness_{ij} = \frac{n_{ij}}{(k_{i} -1) + (k_{j} -1) - n_{ij}}\]

残缺性（dispersion）

残缺度（dispersion， 或译为分散度）是Lars Backstrom & Jon Kleinberg (2013) 为了识别Facebook中亲密关系而提出的度量。它同样是基于共同好友的，主要测量的是共同好友之间的链接缺失程度。

‘dispersion’ — the extent to which two people’s mutual friends are not themselves well-connected. Lars Backstrom & Jon Kleinberg (2013)

Lars Backstrom & Jon Kleinberg使用了脸书的数据发现，使用残缺度这个度量方式，可以非常准确识别诸如夫妻、男女朋友、恋爱关系。

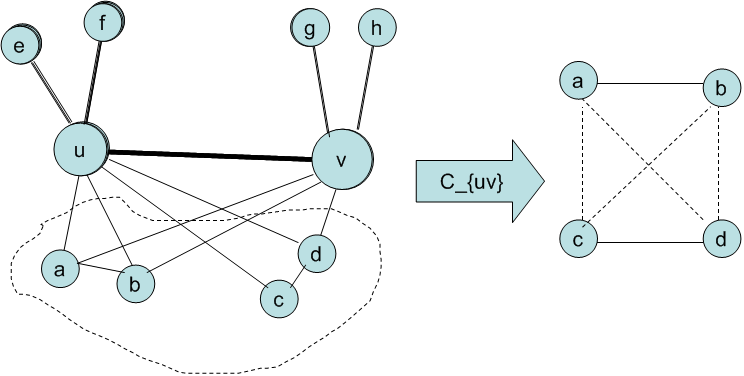
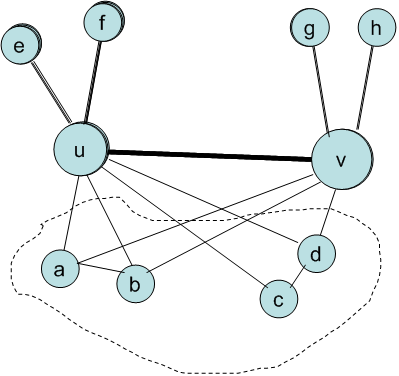
如上图中，u和v两个人有a、b、c、d四个共同好友。残缺度主要考察在多大程度上，这些共同好友不能在两步之内到达彼此。如果两个共同好友之间不存在直接连接，且也不存在（除去u和v之外的）共同好友，那么残缺度就增加1。

以C_{uv}来表示u和v的共同好友之间的链接，那么在上图中只有a、b之间和c、d之间存在链接。a-c, a-d, b-c, b-d四对节点之间既没有直接链接又没有共同好友（除去了u和v)。所以残缺度是4。

再举一个例子，如果u和v的共同好友b-c之间存在直接的链接。那么残缺度会是多大？如下图：

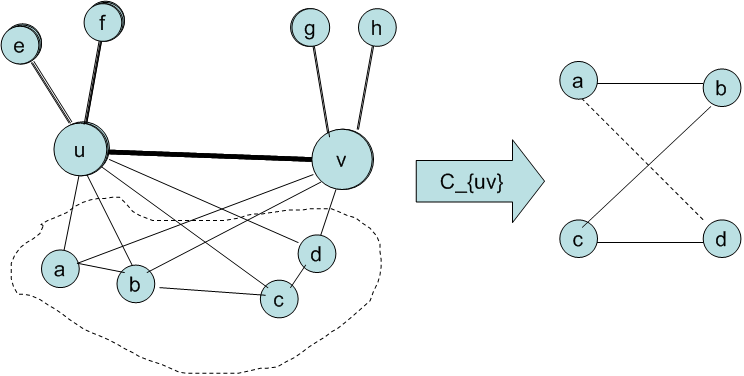
因为只有a-d之间没有办法在两步内到达彼此，所以残缺度是1。

当然了这种定义残缺度的方法是基于节点间的距离的。例如以$d_{s,t}$表示共同好友中任意两个节点s和t之间的距离。在这个初始的定义中，两步内不能到达算是关系残缺。那么我们可以将其扩展为3步内不能到达算残缺，或者n步能不能到达算残缺。不过根据Lars Backstrom & Jon Kleinberg的实验，两步不能到达是一个较好的基准。

如果浪漫关系的确可以由高残缺度刻画，那么说明兔子不吃窝边草在国外是存在的。太熟了下不去手的现象在国内也是存在的。记得一个笑话说：找男女朋友的时候都说找互补的，实际上找到的都是类似的！白富美总是跟高富帅在一起嘛。这应该是对的，人的收入、相貌、工作都是匹配的（match）,从这个角度上讲的确是相似的。但至少从网路结构的角度来说，男女关系依然是互补的！

参考文献

Lars Backstrom & Jon Kleinberg (2013) Romantic Partnerships and the Dispersion of Social Ties: A Network Analysis of Relationship Status on Facebook.arXiv